Newton-Raphson hurbilketa-metodoa ax3+bx2+cx+d=0 ekuazioaren erro bat kalkulatzeko
Matematikan funtzio kubikoa funtzio polinomiko mota bat da, itxura kanonikoan honela definitua:
Non a, b, c eta d (a ≠ 0) zenbaki errealak diren.
Funtzio kubikoaren deribatua funtzio koadratikoa da eta bere integrala funtzio koartikoa da.
Newton–Raphson metodoa (Newton-en metodo gisa ere ezagutzen dena) zenbakizko analisi-metodo bat da. Metodo honek funtzioen erro gero eta hobeak lortzen ditu, hau da, funtzioa zero egiten duen x balioa bilatzen du. Beste modu batez esanik, funtzioak OX ardatza mozten duen balioa (funtzioaren erroa) ematen du Newton–Raphson metodoak. Algoritmoa erroaren hurbilketa batekin hasten da eta urrats bakoitzean erroaren hurbilketa hobea lortzen du.
Aldagai bakarreko funtzio errealen kasuan honakoa da metodoa:
Izan bedi ƒ funtzioa x errealentzat definitua, eta izan bedi ƒ' bere deribatua. Erroaren hasierako hurbilketa bat behar dugu, x0. Erroaren hurbilketa horretan oinarrituz hurbilketa hobea izango den x1 honelaxe lortzen da:
Iterazioak eginez, n+1 hurbilketa n hurbilketan oinarritzen da formula honen arabera:
Formula horren zergatia geometrikoki adieraz daiteke. Hurrengo irudiko lerro urdina f(x) funtzioa da, eta lerro zuzen gorria f(x) funtzioaren tangentea (xn, f(xn)) puntuan:
Berde koloreko distantziari hobekuntza deitzen badiogu, orduan alfa angeluaren tangentea f(xn)/hobekuntza litzateke, baina tangente hori f(x) funtzioaren deribatua (xn, f(xn))puntuan da, lerro zuzen gorriaren malda alfa angeluaren tangentea da. Horregatik:
tag(alfa)= f(xn)/hobekuntza eta aldi berean tag(alfa)=malda= f'(xn)
beraz f'(xn)= f(xn)/hobekuntza (non hobekuntza=xn-xn+1)
f'(xn)= f(xn)/(xn-xn+1) nondik xn-xn+1= f(xn)/f'(xn)
xn+1 = xn - f(xn)/f'(xn)
ax3+bx2+cx+d funtzioaren erro bat kalkula dezagun Newton–Raphson metodoa aplikatuz non a, b, c eta d koefizienteak ezagunak diren. Hona hemen, Newton–Raphson metodotik eratorren formula:
xn+1 = xn - f(xn)/f'(xn)
f(x)=ax3+bx2+cx+d
f'(x)=3ax2+2bx+c
xi+1 = xi - f(xi)/f'(xi)
xi+1 = xi - (axi3+bxi2+cxi+d)/(3axi2+2bxi+c)
Kontu berezia eduki beharko dugu 3axi2+2bxi+c adierazpenaren balioarekin. Ez dugu onartuko zero izatea bestela programa era desegokian bukatuko delako, hots, lehen tangentea ezin daiteke horizontala izan (tangente horrek ez luke OX ardatza moztuko).
Diskriminatzailearen araberako erroak
ax3+bx2+cx+d funtzioaren erroak Δ diskriminatzailearen araberakoak dira. Diskriminatzailea hau da:
Δ = +18·a·b·c·d ‒4·b3·d +b2·c2 ‒4·a·c3 ‒27·a2·d2
ax3+bx2+cx+d funtzioaren erroak Δ diskriminatzailearen arabera:
- Δ > 0, diskriminatzailea positiboa bada, hiru erro desberdin eta errealak. Esate baterako: 1·x3 +2·x2 -5·x -6 = (x+3)·(x+1)·(x-2) polinomioa
- Δ = 0, diskriminatzailea 0 bada, hiru erro erreal (bat doblea eta bestea bakuna, edo bat triplea). Esate baterako: 1·x3 +0·x2 -3·x +2 = (x+2)·(x-1)·(x-1) polinomioa, edo adibidez 1·x3 +3·x2 +3·x +1 = (x+1)·(x+1)·(x+1) polinomioa
- Δ < 0, diskriminatzailea negatiboa bada, erro bat erreala eta beste biak konplexu konjugatuak. Esate baterako: 1·x3 +3·x2 +4·x +12 = (x+3)·(x2+4) polinomioa, edo adibidez antzekoa den 1·x3 +1·x2 -1.5·x +1 = (x+2)·(x2+x+0.5) polinomioa
Diskriminatzaile araberako simulazioak egiteko https://www.geogebra.org/m/WmS455FF webgunea bisita daiteke hurrengo irudietan erakusten den bezala:
ax3+bx2+cx+d funtzioaren erro bat kalkula dezagun, horretarako dagokion ax3+bx2+cx+d=0 ekuazioa formulatu ondoren hasierako x0 hurbilpena teklatuaren bitartez emango dugu Newton–Raphson metodoa aplikatu ahal izateko. Funtzio desberdinen grafikoak marrazteko Google-ren kalkulagailua erabil daiteke. Halaber, polinomio baten faktorizazioa egiteko ondoko bi zerbitzuak erabil daitezke:
ax3+bx2+cx+d=0 ekuazioa
Δ > 0 adibidea, hurrengo irudian x3+12x2-3x-15 funtzioaren itxura ikus daiteke:
Irudiaren gainean klik egin x3+12x2-3x-15 funtzioa aztertzeko
Δ = 0 adibidea, hurrengo irudian (x-2)(x-2)(x+1) funtzioaren itxura ikus daiteke:
Irudiaren gainean klik egin (x-2)(x-2)(x+1) funtzioa aztertzeko
Δ < 0 adibidea, hurrengo irudian (x+2)(x2+x+0.5) funtzioaren itxura ikus daiteke:
Irudiaren gainean klik egin (x+2)(x2+x+0.5) funtzioa aztertzeko
|
NewtonHirugarrenGradukoPolinomioa_HainbatErro.pas ariketa
Algoritmoa:
- Demagun hirugarren graduko polinomioaren rA, rB, rC eta rD koefizienteak teklatuaren bitartez irakurtzen ditugula
- Demagun kalkuluaren rEPSILON doiatsuna konstantea dela eta 0.000000001 balio duela
- Errepikatu erabiltzaileak agindu arte:
- Newton-Raphson metodoa aplikatzeko lehen hurbilketa teklatuaren bitartez irakurri (kontuz puntu horretan tangentearen malda ez dadila 0.0 izan)
- Emandako hurbilketarekin funtzio polinomikoaren erro bat kalkulatu da eta bere balioa pantailaratu
- Beste erro bat kalkulatu nahi den ala ez galdetu
- Erabiltzailearen erantzuna teklatuaren bitartez cErantzuna aldagaian jaso
- Programa amaitu
Balizko soluzio bat programa hau izan daiteke... NewtonHirugarrenGradukoPolinomioa_HainbatErro.pas ...non erro desberdinak kalkulatzen diren galderari B erantzuten zaion bitartean.
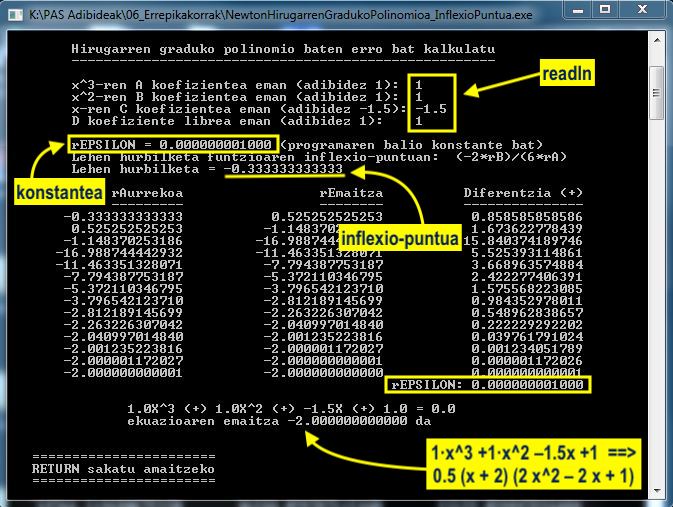
NewtonHirugarrenGradukoPolinomioa_InflexioPuntua.pas ariketa
Funtzio polinomikoarren rA, rB, rC eta rD koefizienteak jaso ondoren eta rEPSILON konstantea izanik, programak erroa kalkula dezala datu geihagorik gabe. Horretako, hasierako hurbilketa egoki bat programak berak aukeratu beharko du.
{ polinomioaren lehen deribatua puntu batean 0.0 bada tangentea puntu }
{ horretan horizontala da eta funtzioaren maximo edo minimo bat dago, }
{ tangentea horizontala bada ezin da Newton-Raphson metodoa aplikatu. }
{ polinomioaren bigarren deribatua 0.0 den puntua inflexio-puntua da, }
{ inflexio-puntua kalkulatu ondoren bere malda 0.0 ez dela konprobatu, }
{ inflexio-puntuan malda 0.0 bada ezin daiteke Newton-Raphson metodoa }
{ erabili, baina inflexio-puntuan tangenteak 0.0 ez badu balio orduan }
{ funtzioaren inflexio-puntua hartu lehendabiziko hurbilketa bezala. }
Algoritmoa:
- Demagun hirugarren graduko polinomioaren rA, rB, rC eta rD koefizienteak teklatuaren bitartez irakurtzen ditugula
- Demagun kalkuluaren rEPSILON doiatsuna konstantea dela eta 0.000000001 balio duela
- Inflexio-puntua kalkulatu:
- Baldin eta lortutako inflexio-puntuan tangenteak 0.0 balio badu, Newton-Raphson metodoa ezin daiteke aplikatu eta horregatik inflexio-puntutik hurbil dagoen beste puntu bat aukeratu beharko da Newton-Raphson metodoaren lehen hurbilketa bezala.
- Bestela, baldin eta lortutako inflexio-puntuan tangenteak 0.0 balio ez badu, Newton-Raphson metodoa erabili non lehen hurbilketa inflexio-puntua izango den
- Lehen hurbilketa zehaztu ondoren, funtzio polinomikoaren erro bat kalkulatu da eta bere balioa pantailaratu
Baina kontuz, inflexio-puntuaren tangenteak 0.0 balio badu. Halako kasuan, inflexio-puntutik hurbil dagoen beste bat aukeratu Newton-Raphson metodoaren lehen hurbilketa bezala. Esate baterako, lehen hurbilketa aukeratzeko rEPSILON lagungarria izan daiteke, ondoko irudian erakusten den bezala:
Balizko soluzio bat programa hau izan daiteke... NewtonHirugarrenGradukoPolinomioa_InflexioPuntua.pas ...non rEPSILON doitasuna 0.000000001 konstantea den.



















iruzkinik ez:
Argitaratu iruzkina
Iruzkinen bat idazteko Google-ko kontu bat behar duzu. Iruzkin guztien moderazio-ardura blogeko administratzaileari dagokio.